Il primo passo da fare è sicuramente tradurre in un modello matematico/meccanico quello che vediamo, ad esempio in campo automobilistico, i primo modelli sono stati ad esempio il quarter-car che fa parte della famiglia dei modelli ride che permettono di simulare la risposta di una vettura al variare delle asperità del terreno o del carico trasportato.
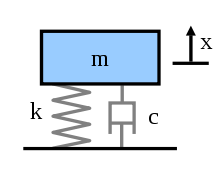
Essenzialmente quello che fanno questi modelli base è approssimare il veicolo a un unico sistema massa-molla-smorzatore, le tre componenti principali di questo sistema come già detto sono:
-Massa, la quale tiene conto degli effetti inerziali
-Smorzatore, tiene conto delle dissipazioni energetiche come attriti e resistenza aerodinamiche.
-Molla, tiene conto della componente elastiche del sistema.
Avremo quindi un sistema del genere:
La frequenza naturale o pulsazione naturale è proporzionale alla rigidezza del sistema e inversamente proporzionale alla massa, quindi sistemi non molto rigidi e con massa elevate hanno basse pulsazioni di risonanza e viceversa sistemi molto rigidi e con poca massa hanno elevate pulsazioni naturali.
Il rapporto di smorzamento indica quanto il sistema è smorzato, ovvero con rapporti maggiori o uguali a uno, il sistema molto smorzato, se invece il rapporto è prossimo allo zero, il sistema è poco smorzato.
Nel caso di un veicolo ci troviamo di solito davanti a pulsazioni naturali non molto elevate, rispetto a quelle di sistemi elettronici e rapporti di smorzamento bassi.
Vediamo ora come queste conoscenze di base ci possono essere utili, prendiamo un sistema ride molto semplice con un solo grado di libertà come quello illustrato sopra e andiamo a sollecitarlo.
Possiamo fare due scelte:
-Andare a imporre uno spostamento della base e osservare come varia la posizione x, come ad esempio succede quando un veicolo incontra un’asperità.
-Applicare direttamente una forza sulla massa e osservare la variazione della posizione x nel tempo.
Sollecitazione Sinusoidale
La sollecitazione più interessante da applicare è sicuramente un ingresso di tipo sinusoidale, questo perché una qualsiasi forma della strada o una forza con andamento generico può facilmente essere trasformata con un la trasformata di Fourier in una somma di ingressi di tipo sinusoidale, ognuno con la propria frequenza.
Andiamo alla parte interessante, è facilmente dimostrabile matematicamente che nel caso di sistemi meccanici reali la risposta che otteniamo è nuovamente di tipo sinusoidale e possiede le seguenti caratteristiche.
Il sistema inizierà ad oscillare con una pulsazione minore della pulsazione naturale del sistema, che chiameremo frequenza di risonanza, più il rapporto di smorzamento è elevato e più questa frequenza è bassa e si allontana quindi dalla frequenza naturale.
Il sistema si muove con un certo ritardo che va via via aumentando all’aumentare della frequenza della sollecitazione.
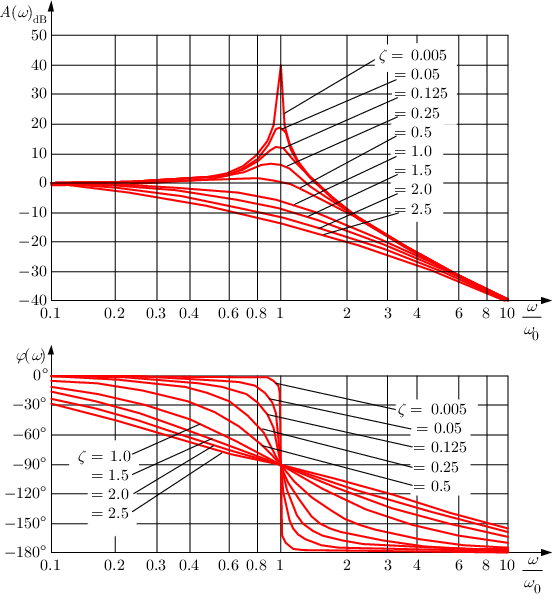
Anche l’ampiezza dell’oscillazione dipende fortemente dalla frequenza, se molto bassa risulta circa costante, presenta massima ampiezza alla frequenza di risonanza, e poi scende via via, importante notare come se il rapporto di smorzamento è più elevato di 0.7, non compare più il picco di risonanza e non è possibile più definire nemmeno la frequenza di risonanza, questo perché il sistema diventa troppo smorzato e non oscilla più.
Tutte queste caratteristiche possono essere riassunte in unico diagramma, il diagramma di Bode, in cui A(w) rappresenta l’ampiezza dell’oscillazione, mentre l’altro diagramma rappresenta a grandi linee quanto in ritardo è la risposta.
Finita questa parte introduttiva andiamo a vedere bene cosa succede con modelli più complessi.
Modelli a più gradi di libertà.
Un approccio più sofisticato prevede di non utilizzare più un modello a un solo grado di libertà come quella su cui abbiamo ragionato finora, ma più gradi di libertà, ad esempio nelle simulazione delle dinamiche di aeromobili si usano fino a 2 miliardi di gradi di libertà.
La differenza principale è che un sistema con n gradi di libertà presenta n frequenze naturali e di risonanze n modi naturali di vibrare, il moto complessivo non è altro che la somma di tutti questi modi di vibrare combinati tra loro.
Facciamo un esempio, prendiamo un e consideriamo il beccheggio, un primo modo naturale è quello in cui oscillano in maniera alternata la parte anteriore e posteriore, un secondo modo di vibrare è l’oscillazione simultanea.
Il moto complessivo quindi sarà una composizione di questi due modi naturali, analogamente per n gradi di libertà.
In base alla frequenza predominante della sollecitazione quindi si andrà attivare uno o l’altro modo di vibrare con conseguenti diverse dinamiche di oscillazione, in generale le prime frequenze di risonanza (quelle più basse) sono quelle con maggior contenuto e con le ampiezze più elevate, mentre le altre hanno minor contenuto energetico e minor ampiezza.
Un altro esempio per chiarire questo fatto, il famoso ponte Tacoma Narrows, in questo caso l’azione del vento andò ad eccitare proprio uno di questi modi a bassa frequenza con conseguenza catastrofiche, l’ampiezza dell’oscillazione portò infatti alla rottura del ponte.
Sui veicoli normalmente è difficile trovare sollecitazioni a cosi bassa frequenza, di solito si ha a che fare con sollecitazioni a più alta frequenza che portano più a vibrazioni che vere e proprie oscillazioni.
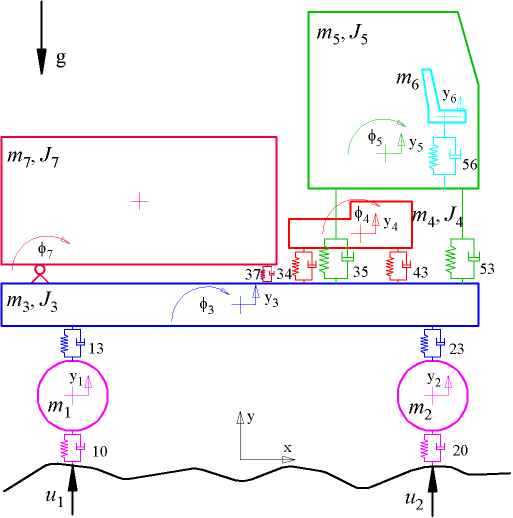
Esempio di modello a più gradi di libertà.